C++ 算法篇 位运算

学习目标

1. 理解与掌握 C++ 中的位运算。
2. 灵活应用位运算优化程序。

任何信息在计算机中都是采用二进制表示的，数据在计算机中是以补码形式存储的，位运算就是直接对整数在内存中的二进制位进行运算。由于位运算直接对内存数据进行操作，不需要转换成十进制，因此处理速度非常快，在信息学竞赛中往往可以优化理论时间复杂度的系数。同时，一个整数的各个二进制位互不影响，利用位运算的一些技巧可以帮助我们简化程序代码。

一、位运算符

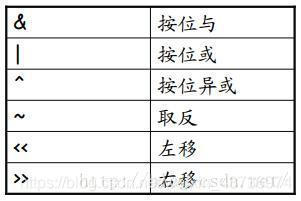
C++ 提供了按位与（\&）、按位或（| ）、按位异或（\^）、取反（\~）、左移（\<\<）、右移（>>）这 6 种位运算符。 这些运算符只能用于整型操作数，即只能用于带符号或无符号的 char、short、int 与 long 类型。

（一）按位与运算符（\&）

“a\&b”是指将参加运算的两个整数a和b，按二进制位进行”与”运算。

运算规则：0\&0=0; 0\&1=0; 1\&0=0; 1\&1=1; 即：两位同时为”1″，结果才为”1″，否则为0

例如：3\&5 即 0000 0011\& 0000 0101 = 0000 0001 因此，3\&5的值得1。

另，负数按补码形式参加按位与运算。

按位与\&比较实用的例子：

1. 比如我们经常要用的是否被2整除，一般都写成 if(n
2. 按位与运算可以取出一个数中指定位。例如：要取出整数84从左边算起的第3、4、5、7、8位，只要执行84 \& 59,因为84对应的二进制为01010100，59对应的二进制为00111011，01010100 \& 00111011= 00010000 可知84从左边算起的第3、4、5、7、8位分别是0、1、0、0、0。
3. 清零。如果想将一个单元清零，使其全部二进制位为0，只要与一个各位都为零的数值相与，结果为零。

1. 整数幂：

判断一个数n ，是不是2的整数幂。比如：64＝2\^6,所以输出”yes”,而65无法表示成2的整数幂的形式，所以输出”NO”。

#include<bits/stdc++.h>
using namespace std;
int main()
{  int n;
   cin>>n;
   if(n&(n-1))cout<<"NO";
   else cout<<"Yes";
}

2. 计算一个数的二进制中1的个数:

算法1：通过与初始值为1的标志位进行与运算，判断最低位是否为1；然后将标志位左移，判断次低位是否为1；一直这样计算，直到将每一位都判断完毕。

#include<bits/stdc++.h>
using namespace std;
int main()
{   int n = 0,num;
    unsigned int flag = 1;
    cin>>num;
    while(flag)
    {   if(num & flag) n++;
        flag = flag << 1;
    }
    cout<<n;
}

算法2：还有一种方法，一个整数减一，可以得到该整数的最右边的1变为0，这个1右边的0变为1。对这个整数和整数减一进行与运算，将该整数的最右边的1变为0，其余位保持不变。直到该整数变为0，进行的与运算的次数即为整数中1的个数。

#include<bits/stdc++.h>
using namespace std;
int main()
{   int n = 0,num;
    unsigned int flag = 1;
    cin>>num;
    while(num)
    {   num = num & (num - 1);
        n++;
    }
    cout<<n;
}

（二）按位或运算符（|）

参加运算的两个对象，按二进制位进行”或”运算。

运算规则：0|0=0； 0|1=1； 1|0=1； 1|1=1；

即 ：参加运算的两个对象只要有一个为1，其值为1。

例如:3|5　即 00000011 | 0000 0101 = 00000111 因此，3|5的值得7。　 另，负数按补码形式参加按位或运算。

按位或 （|） 比较实用的例子

可以用一个unsigned int 来存储多个布尔值。比如一个文件有读权限，写权限，执行权限。看起来要记录3个布尔值。我们可以用一个unsigned int也可以完成任务。

一个数r来表示读权限，它只更改个位来记录读权限的布尔值 00000001 (表示有读权限) 00000000 (表示没有读权限)

一个数w表示写权限，它只用二进制的倒数第二位来记录布尔值 00000010 (表示有写权限) 00000000 (表示没有写权限)

一个数x表示执行权限，它只用倒数第三位来记录布尔值 00000100 (表示有执行权限) 00000000 (表示没有执行权限)

那么一个文件同时没有3种权限就是 \~r | \~ w | \~ x 即为 00000000，就是0

只有读的权限就是 r | \~w | \~x 即为 00000001，就是1

只有写的权限就是 \~r | w | \~x 即为 00000010，就是2

一个文件同时有3种权限就是 r | w | x 即为 00000111，就是7

（三）按位异或运算符（\^）

参加运算的两个数据，按二进制位进行”异或”运算。

运算规则：0 \^ 0=0； 0 \^ 1=1； 1\^ 0=1； 1\^1=0；

即：参加运算的两个对象，如果两个相应位为”异”（值不同），则该位结果为1，否则为0。

下面重点说一下按位异或,异或 其实就是不进位加法,如1+1=0，,0+0=0,1+0=1。

异或的几条性质:

1. 交换律:a \^ b=b \^ a
2. 结合律:(a \^ b) \^ c a\^ (b \^ c)

“异或运算”的特殊作用：

1. 使特定位翻转: 例：X=10101110，使X低4位翻转，用X \^ 0000 1111 = 1010 0001即可得到。
2. 与0相异或，保留原值 ，10101110\^ 00000000 = 1010 1110。
3. 对于任何数x都有――自反性:x\^ x=0，x\^ 0=x 例如：A\^B \^ B = A
4. 交换二个数：a =a \^ b; b = b \^ a; a = a \^ b;

1. 奇偶数

给出 n 个整数，n 为奇数，其中有且仅有一个数出现了奇数次，其余的数都出现了偶数次。用线性时间复杂度、常数空间复杂度找出出现了奇数次的那个数。

【输入样例】

9

3 3 7 2 4 2 5 5 4

【输出样例】

7

#include<bits/stdc++.h>
using namespace std;
int main()
{   int i,n,m,a;
    cin>>n;
    cin>>a;
    for(int i = 2; i <= n; i++) 
    {cin>>m; a^=m;   }
    cout<<a<<endl;
}

2. 寻找重复数字

1-1000放在含有1001个元素的数组中，只有唯一的一个元素值重复，其它均只出现 一次。每个数组元素只能访问一次，设计一个算法，将它找出来；不用辅助存储空间，能否设计一个算法实现？

解法一、显然已经有人提出了一个比较精彩的解法，将所有数加起来，减去1+2+…+1000的和。

这个算法已经足够完美了，相信出题者的标准答案也就是这个算法，唯一的问题是，如果数列过大，则可能会导致溢出。

解法二、异或就没有这个问题，并且性能更好。

将所有的数全部异或，得到的结果与1\^2\^3\^…\^1000的结果进行异或，得到的结果就是重复数。

​

#include<bits/stdc++.h>
using namespace std;
int main()
{  int i,n,a[11]={1,2,5,3,4,5,6,7,8,9,10};
   n=a[0]^a[1];
  for(i=2;i<=10;i++)n=n^a[i]; 
  for(i=1;i<=10;i++)n=n^i;
  cout<<n;
}

3. 寻找单独数字

一系列数中,除两个数外其他数字都出现过两次,求这两个数字,并且按照从小到大的顺序输出.例如 2 2 1 1 3 4.最后输出的就是3 和4

#include<bits/stdc++.h>
using namespace std;
int a[1000];
int main()
{       int n;
        scanf("
        int x = 0;
        for(int i = 1; i <= n; i++) {      scanf("
        int num1 = 0, num2 = 0;
        int tmp = 1;
        while(!(tmp & x)) tmp <<= 1;
        cout<<tmp<<endl;
        for(int i = 1; i <= n; i++) {
            if(tmp & a[i]) num1 ^= a[i];
            else num2 ^= a[i];
        }
        printf("
    return 0;
}

（四）按位取反运算符（\~）

按位取反运算符（\~）是指将整数的各个二进制位都取反，即1变为0，0变为1。

例如，\~9＝－10，因为9（00001001）所有位取反即为（11110110），这个数最高位是1，所以是补码。补码还原成反码（反码等于补码减1）得到（11110101），再还原为原码（反码到原码最高位不变，其它各位取反）等于（10001010）， 十进制为－10。

（五）按位左移运算符（\<\<）

左移运算符是用来将一个数的各二进制位左移若干位，移动的位数由右操作数指定（右操作数必须是非负值），其右边空出的位用0填补，高位左移溢出则舍弃该高位。

在高位没有1的情况下，左移1位相当于该数乘以2，左移2位相当于该数乘以2*2＝4,15＜＜2=60，即乘了４。
但此结论只适用于该数左移时被溢出舍弃的高位中不包含1的情况。

例如：143\<\<2 结果为60 因为143转换为进制为10001111，左移2得00111100 ，结果为60。

（六）按位右移运算符（>>）

右移运算符是用来将一个数的各二进制位右移若干位，移动的位数由右操作数指定（右操作数必须是非负值），移到右端的低位被舍弃，对于无符号数，高位补0。对于有符号数，某些机器将对左边空出的部分用符号位填补（即”算术移位”），而另一些机器则对左边空出的部分用0填补（即”逻辑移位”）。

注意：对无符号数,右移时左边高位移入0；对于有符号的值,如果原来符号位为0(该数为正),则左边也是移入0。如果符号位原来为1(即负数),则左边移入0还是1,要取决于所用的计算机系统。有的系统移入0,有的系统移入1。移入0的称为”逻辑移位”,即简单移位；移入1的称为”算术移位”。

例： a的值是八进制数113755：

a:1001011111101101 （用二进制形式表示）

a>>1: 0100101111110110 (逻辑右移时)

a>>1: 1100101111110110 (算术右移时)

在有些系统中,a>>1得八进制数045766,而在另一些系统上可能得到的是145766。Turbo C和其他一些C编译采用的是算术右移,即对有符号数右移时,如果符号位原来为1，左面移入高位的是1。

源代码：

#include \<stdio.h\>  
main()  
{ int a=0113755; printf("

（七）位运算优先级

总的来说比较低，逻辑运算符和数学运算符出现在同一个表达式中，那么需要用括号来表达运算次序。

（八）复合赋值运算符

位运算符与赋值运算符结合，组成新的复合赋值运算符，它们是：

1. \&= 例：a \&=b 相当于a=a\& b
2. |= 例：a |=b 相当于a=a |b
3. >>= 例：a >>=b 相当于a=a>> b
4. \<\<= 例：a\<\<=b 相当于a=a\<\< b
5. \^= 例：a \^= b 相当 a=a \^b

运算规则：和前面讲的复合赋值运算符的运算规则相似。

（九）不同长度的数据进行位运算

如果两个不同长度的数据进行位运算时，系统会将二者按右端对齐，然后进行位运算。

以”与”运算为例说明如下：如果一个4个字节的数据与一个2个字节数据进行”与”运算，右端对齐后，左边不足的位依下面三种情况补足：

1. 如果整型数据为正数，左边补16个0。
2. 如果整型数据为负数，左边补16个1。
3. 如果整形数据为无符号数，左边也补16个0。

（十）下面列举一些常见的二进制位的变换操作

操作	演示	代码
去掉最后一位	101101->10110	x>>1
在最后加一个0	101101->1011010	x\<\<1
在最后加一个1	101101->1011011	(x\<\<1)+1
把最后一位变成1	101100->101101	x | 1
把最后一位变成0	101101->101100	(x |1) – 1
最后一位取反	101101->101100	x \^ 1
把右数第K位变成1	101001->101101,k=3	x | (1\<\<(k-1))
把右数第K位变成0	101101->101101,k=3	x \& \~(1\<\<(k-1))
右数第k位取反	101001->101101,k=3	x \^ (1\<\<(k-1))
取末三位	1101101->101	x \&7
取末k位	1101101->1101,k=5	x \& (1\<\<k-1)
取右数第k位	1101101->1,k=4	x >> (k-1)\&1
把末k位变成1	101001->101111,k=4	x|(1\<\<k-1)
末k位取反	101001->100110,k=4	x\^(1\<\<k-1)
把右边连续的1变成0	100101111->100100000	x\&(x+1)
把右起第一个0变成1	100101111->100111111	x|(x+1)
把右边连续的0变成1	11011000->11011111	x|(x-1)
取右边连续的1	100101111->1111	(x\^(x+1))>>1
去掉右起第一个1的左边	100101000->1000	x\&(x\^(x-1))

最后一个会在树状数组中用到