注意力机制

余弦相似度

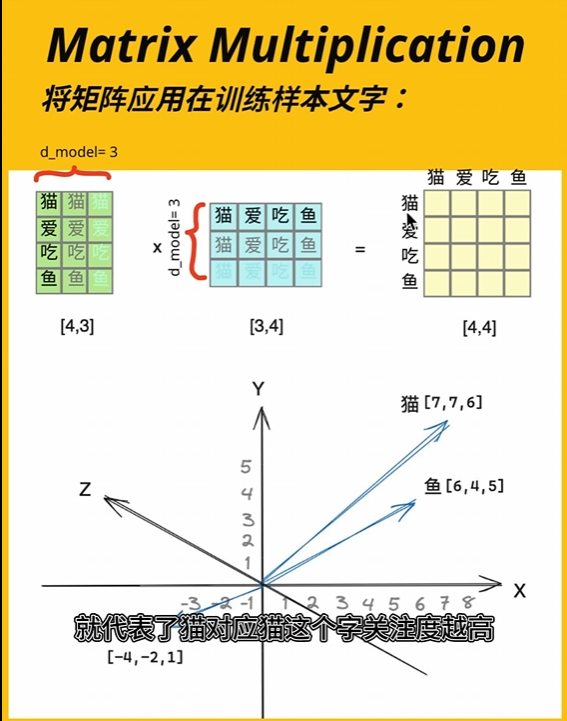
余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦相似度通常用于正空间，因此给出的值为0到1之间。

层归一化（Layer Normalization）

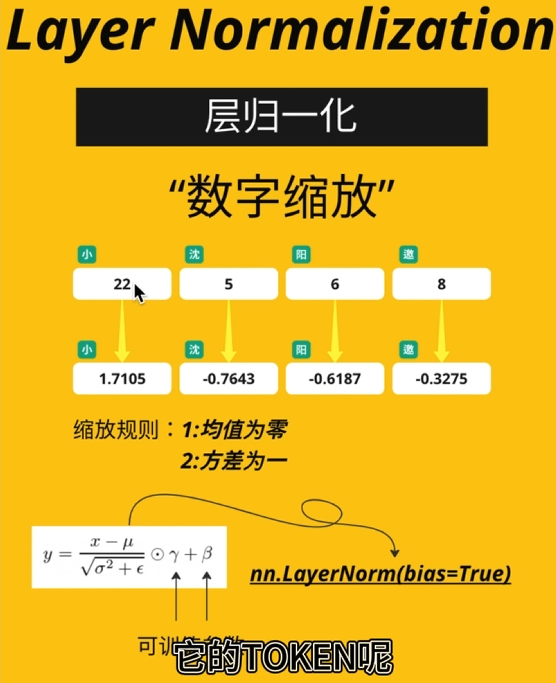
作用：对单个样本的所有特征进行标准化，加速训练。
步骤：
1. 计算均值与方差：
  $$
  \mu=\frac{1}{H}\sum_{h=1}^Hx_h,\quad\sigma^2=\frac{1}{H}\sum_{h=1}^H(x_h-\mu)^2
  $$
2. 标准化并应用缩放和平移：
  $$
  y=\gamma\cdot\frac{x-\mu}{\sqrt{\sigma^{2}+\epsilon}}+\beta\
  $$
  其中，$H$为特征维度，$\gamma$和 $\beta$ 为可学习参数，$\epsilon $为小常数（防除零）。

softmax

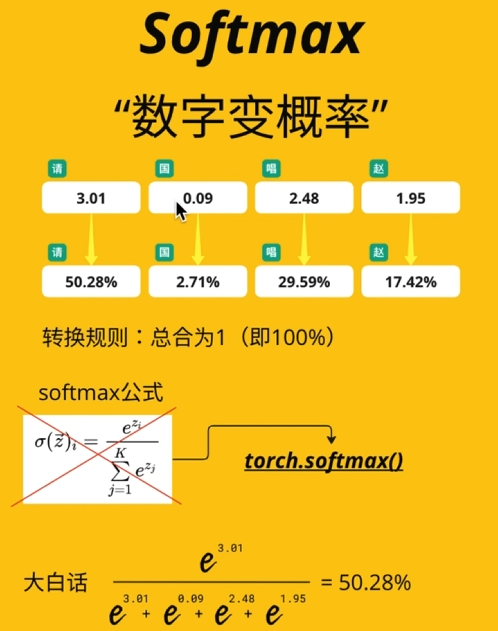
作用：将向量转换为概率分布，总和为1。
公式：
$$
\sigma(z_i)=\frac{e^{z_i}}{\sum_{j=1}^Ke^{z_j}}
$$
其中$z$是输入向量，$K$为类别数，$\sigma(z_i)$表示第$i$类的概率。

QKV

准备QKTV

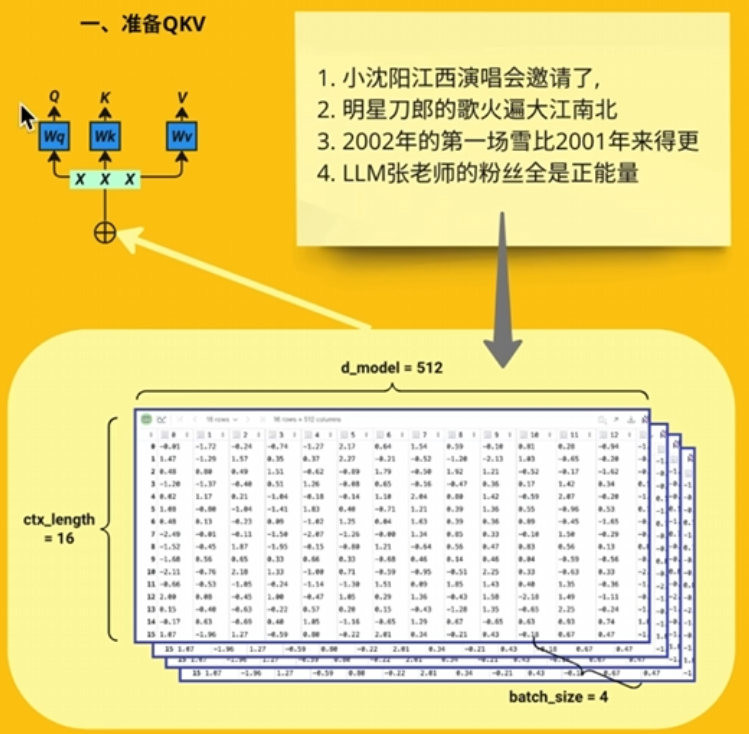
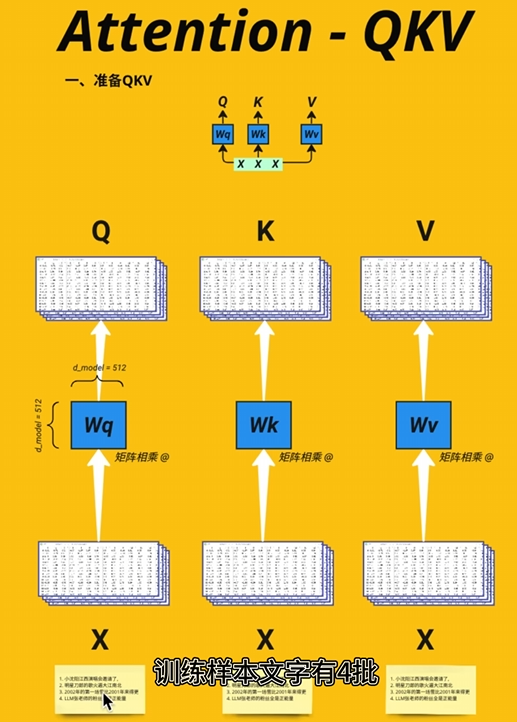
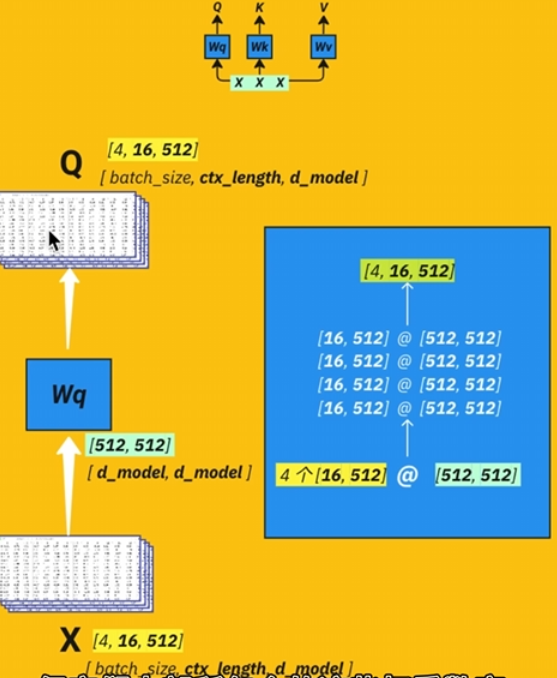
把数据加入权重，权重形状【512，512】，分成三份用于计算。

切分多头

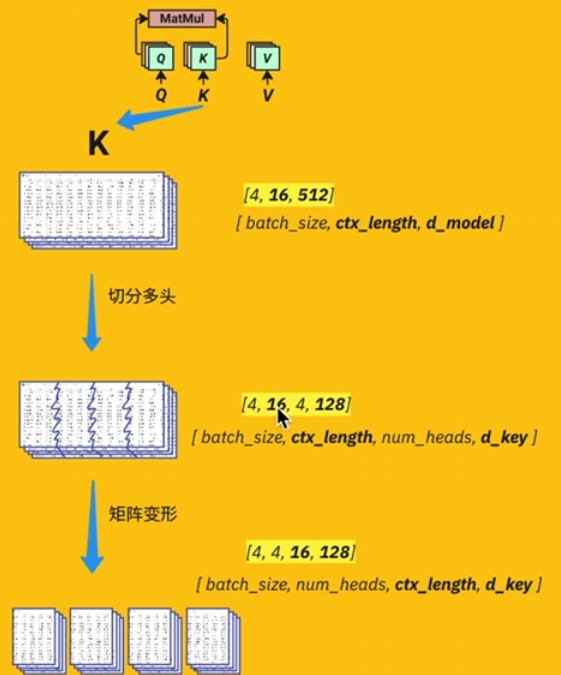
将512个特征值切分成【4，128】

为什么要拆分多头注意力？

多样化特征捕捉：每个头关注输入的不同子空间，学习不同的注意力模式（如局部依赖、长程关联等），提升模型捕捉复杂特征的能力。

并行计算效率：拆分后各头可独立计算注意力，充分利用GPU等硬件的并行计算能力，加速训练。

降低维度复杂度：将高维特征拆分为多个低维子空间，减少单头注意力矩阵的计算量（复杂度从 $O(L^2d)$ 降至 $O(L^2d/h)$。

(Q, K)@V注意力

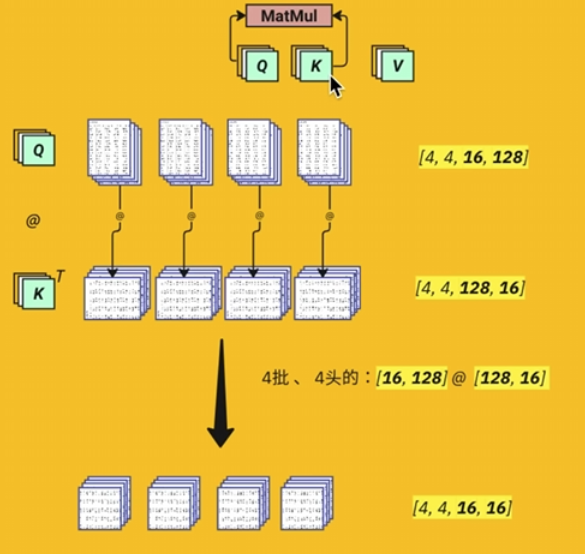
将K转置，与Q相乘。为避免避免因高维点积导致的梯度消失或爆炸，进行点积缩放，保持点积方差与维度无关，避免 Softmax 失效。
$$
\mathrm{Attention}(Q,K,V)=\mathrm{softmax}(\frac{QK^{T}}{\sqrt{d_{key}}})V
$$

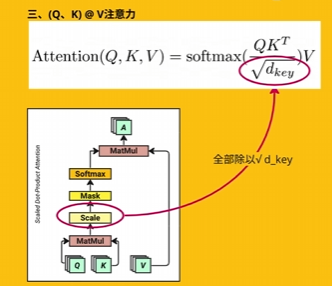
数学推导

1.假设条件：

查询$Q$和键$K$的每个元素独立，均值为0，方差为$\sigma^{2}$。

2.点积方差计算：

$$
\mathrm{Var}(Q_iK_j)=\mathbb{E}[Q_i^2K_j^2]-(\mathbb{E}[Q_iK_j])^2=\sigma^4
$$

由于$Q\cdot K^T=\sum_{i=1}^{d_k}Q_iK_i$,其方差为：

$$
\mathrm{Var}(Q\cdot K^T)=d_k\cdot\sigma^4
$$

3.缩放后的方差：
$$
\mathrm{Var}\left(\frac{Q\cdot K^T}{\sqrt{d_k}}\right)=\frac{d_k\cdot\sigma^4}{d_k}=\sigma^4
$$