生成模型
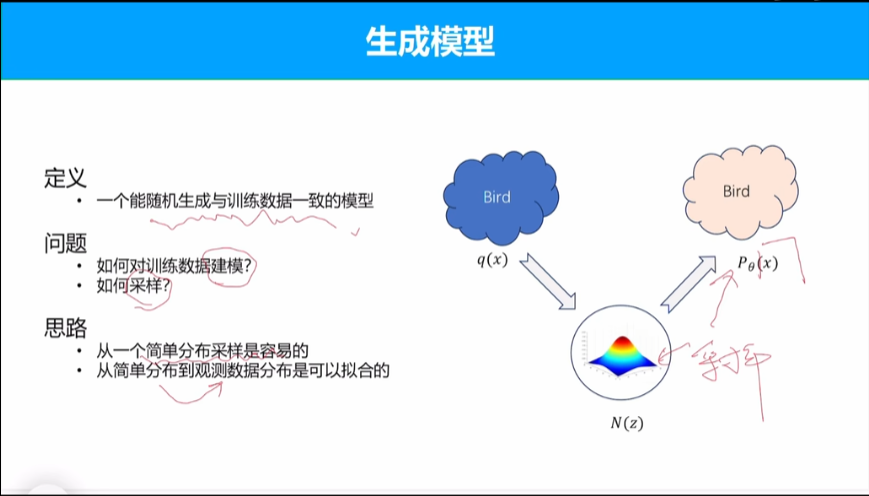
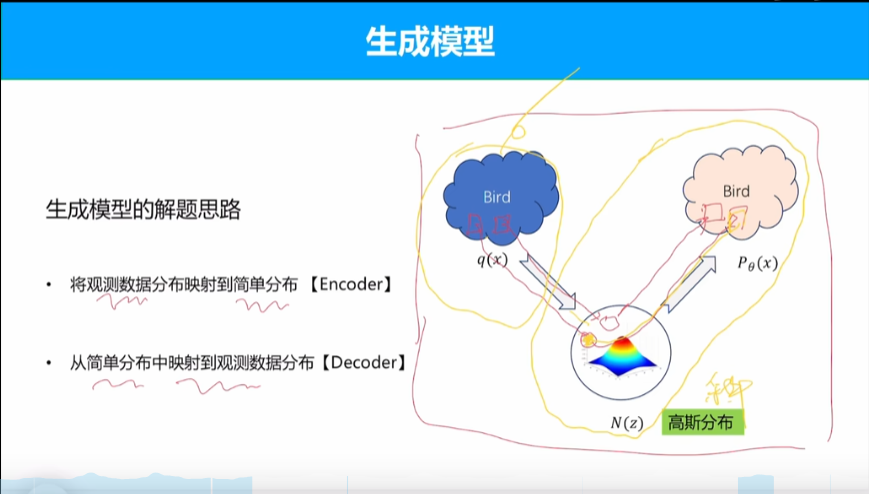
基本思路是使用一个简单分布作为桥梁,将观测数据分布映射到简单分布中,再从简单分布映射观测数据分布。
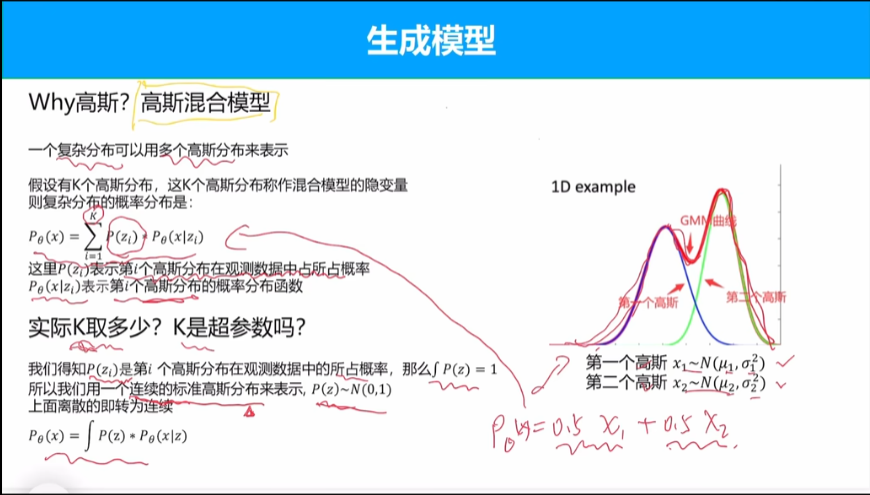
使用高斯分布是因为高斯函数的运算性质很方便,也比较简单。多个高斯分布可以拟合一个复杂的分布。

扩散过程人为定义,反向生成过程引入参数\theta,根据最大似然估计方法,转化为求下界的上限。
DDPM
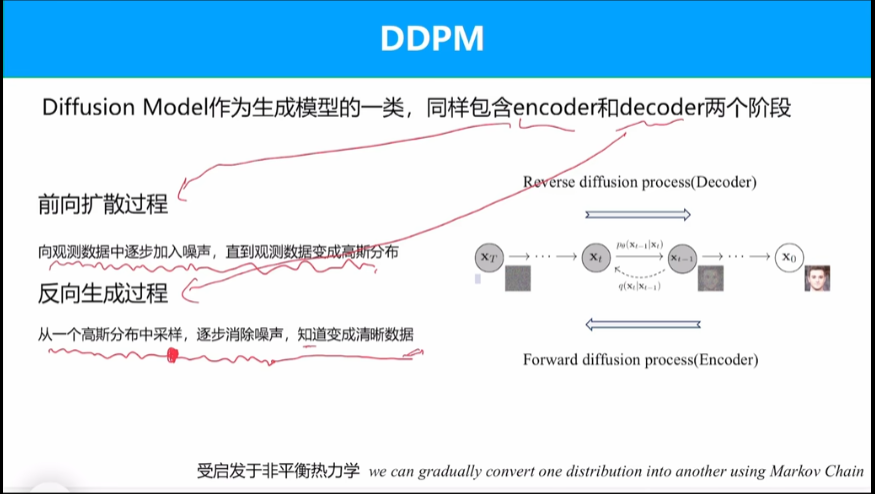
前向扩散过程
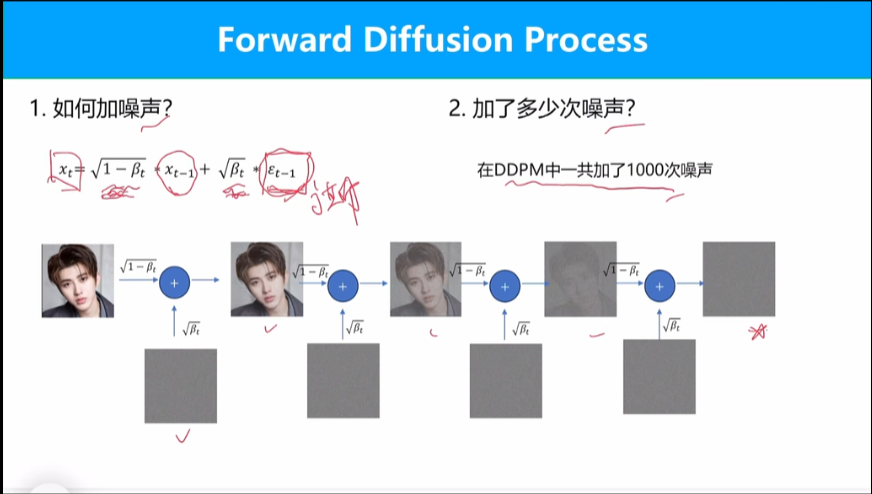
扩散模型的话通过超参数\beta将清晰图片和噪声图片加权求和,达到添加噪声的目的。
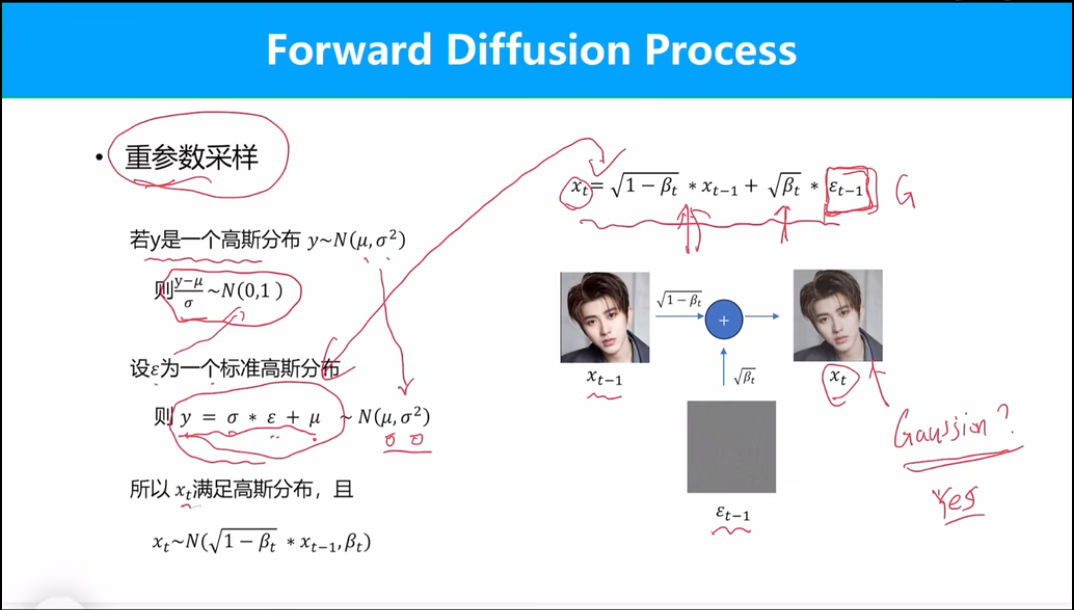
对于加权求和的结果,根据重参数采样,依然符合高斯分布。
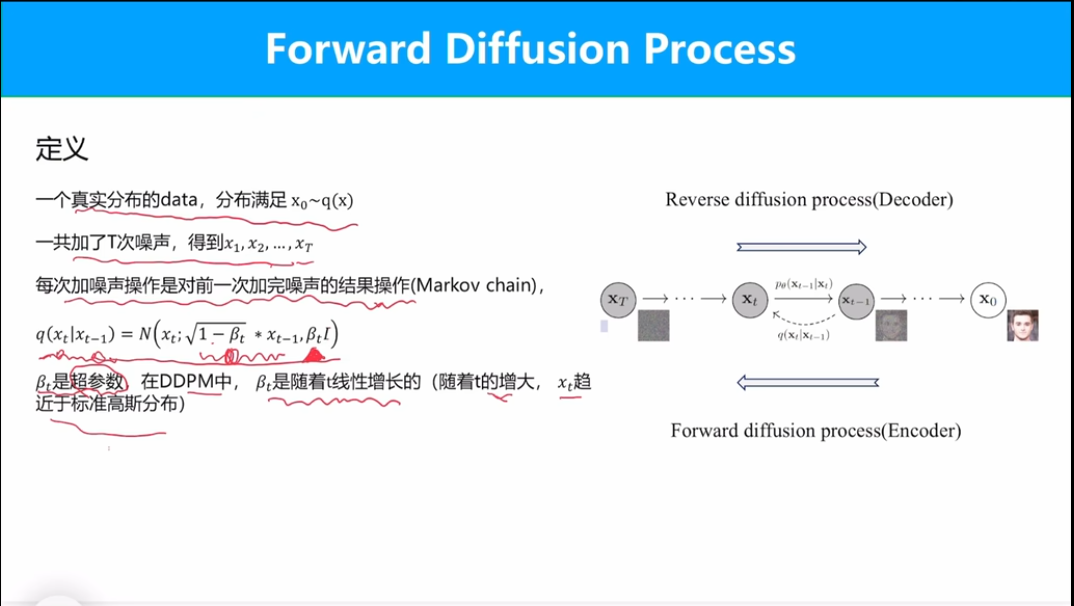
对于超参数\beta,原始论文中设置为随着时间步t线性增长。

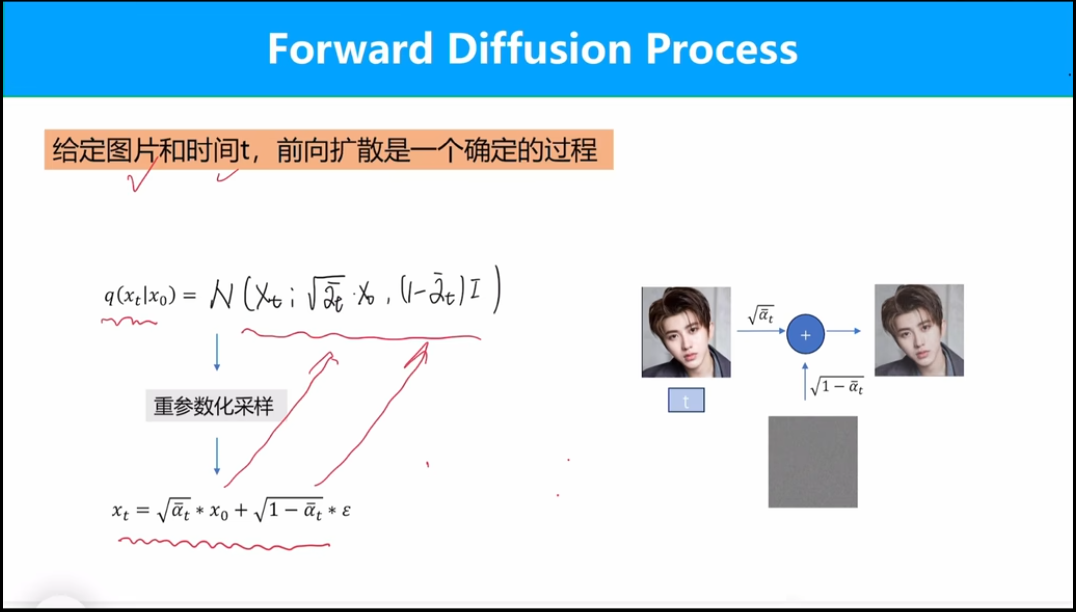
每一个时间步中随机生成的高斯分布相互独立,他们的加权求和依然是高斯分布,超参数更改为用\alpha表示。
反向生成过程
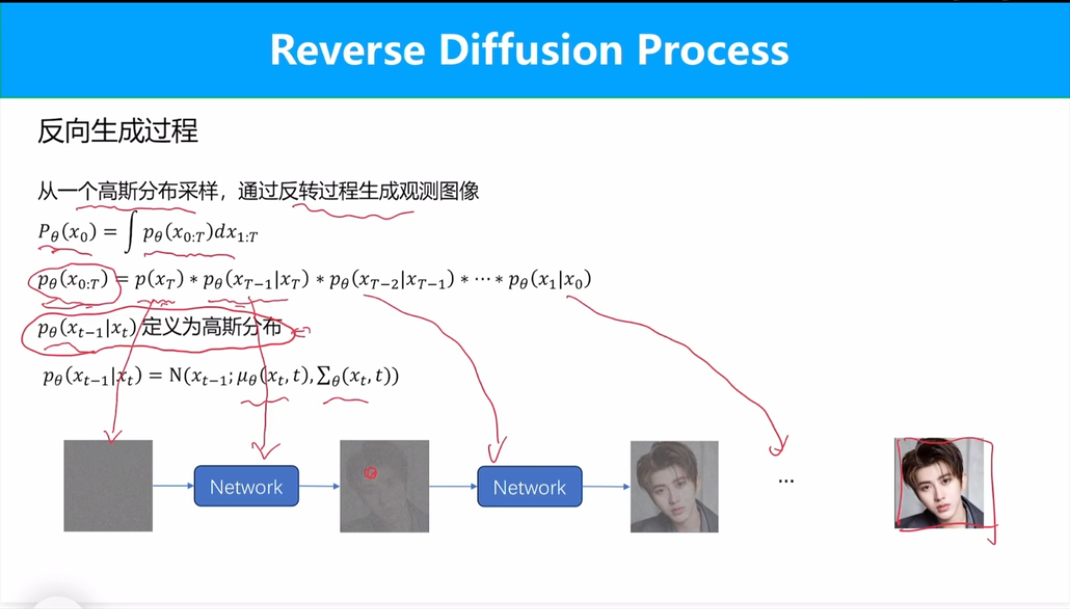
现在希望从高斯分布中采样生成x_0清晰图像。假设采样过程逐步进行,最终由噪声图像x_t生成清晰图像x_0分布由每一时间步的分布累乘。
定义每一时间步的反向生成过程符合高斯分布,则整个反向生成过程也符合高斯分布。


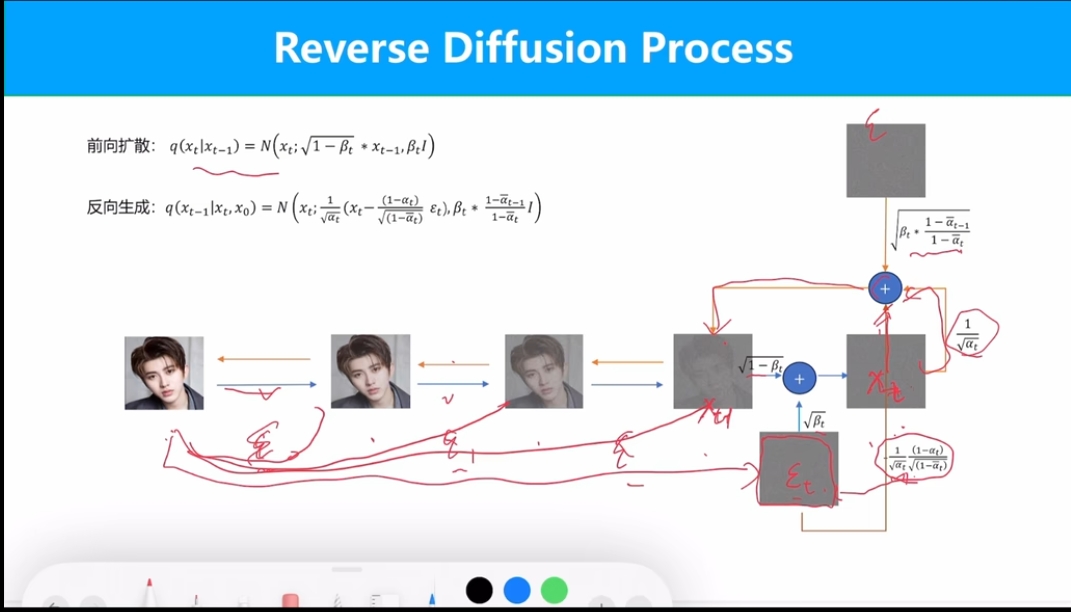
反向生成过程的均值和方差如上。已知x_0和x_t时,整个分布已知确定。
优化目标
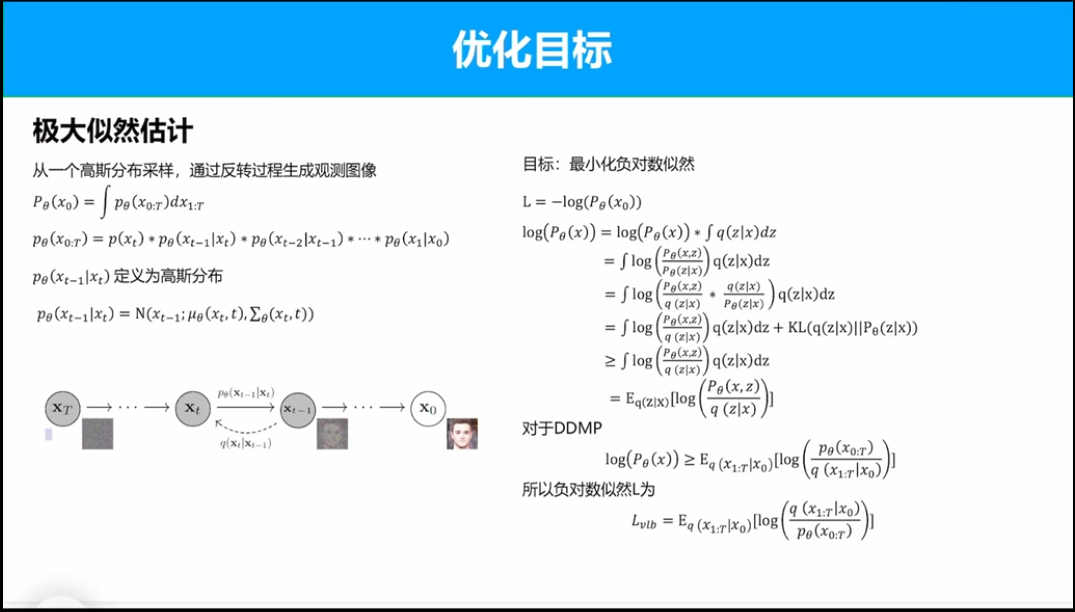


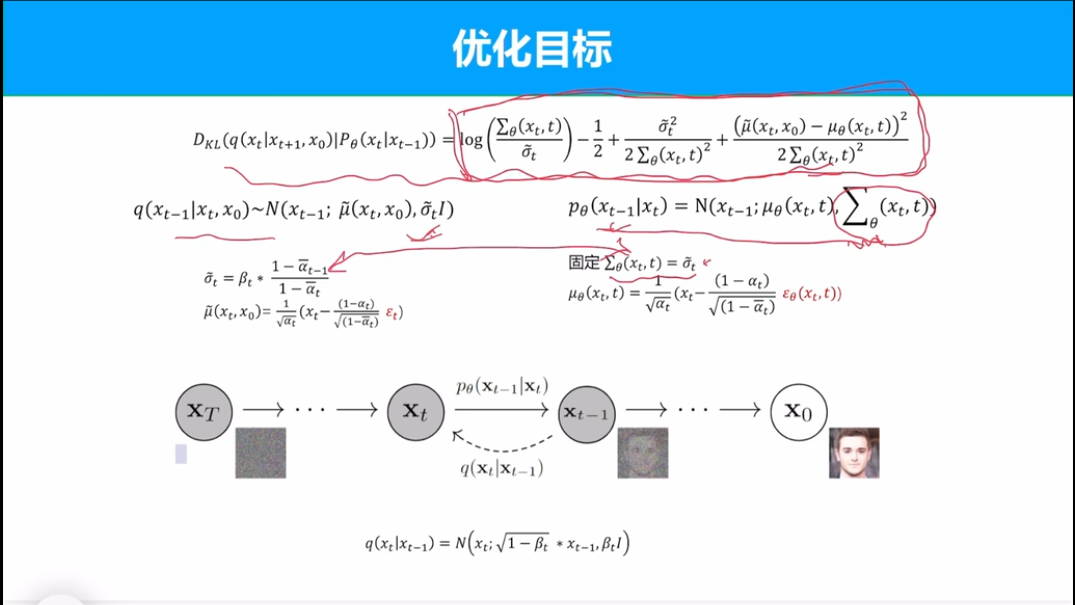
对于优化目标和扩散过程类似,目的是求去下界的上限。在原论文中,作者假设扩散生成两个过程方差不变,loss结果如下。
训练推理算法
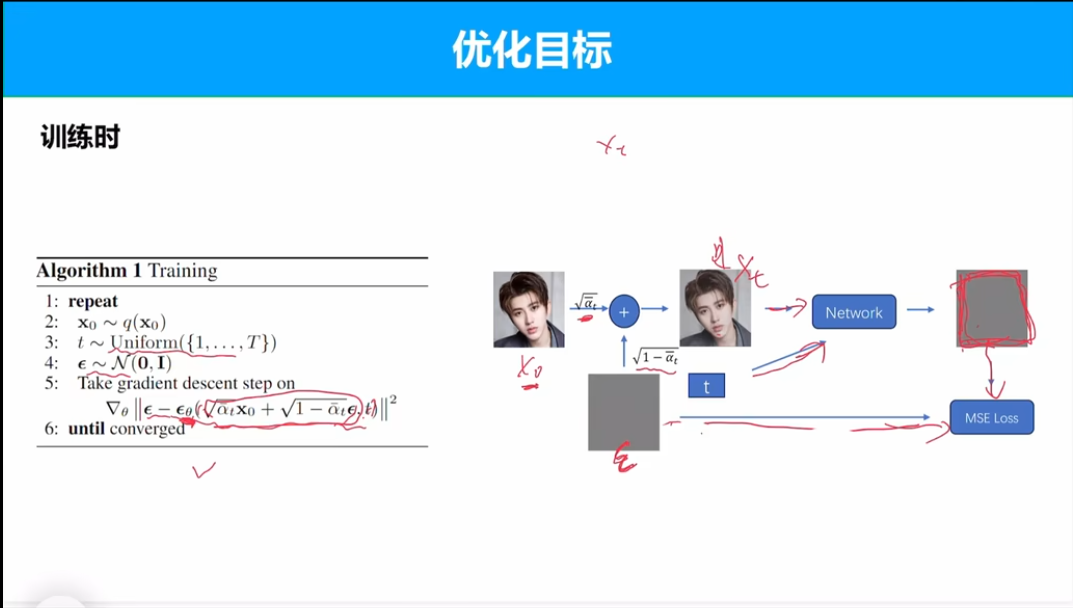
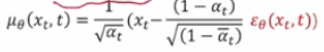
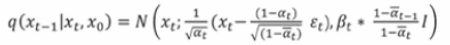
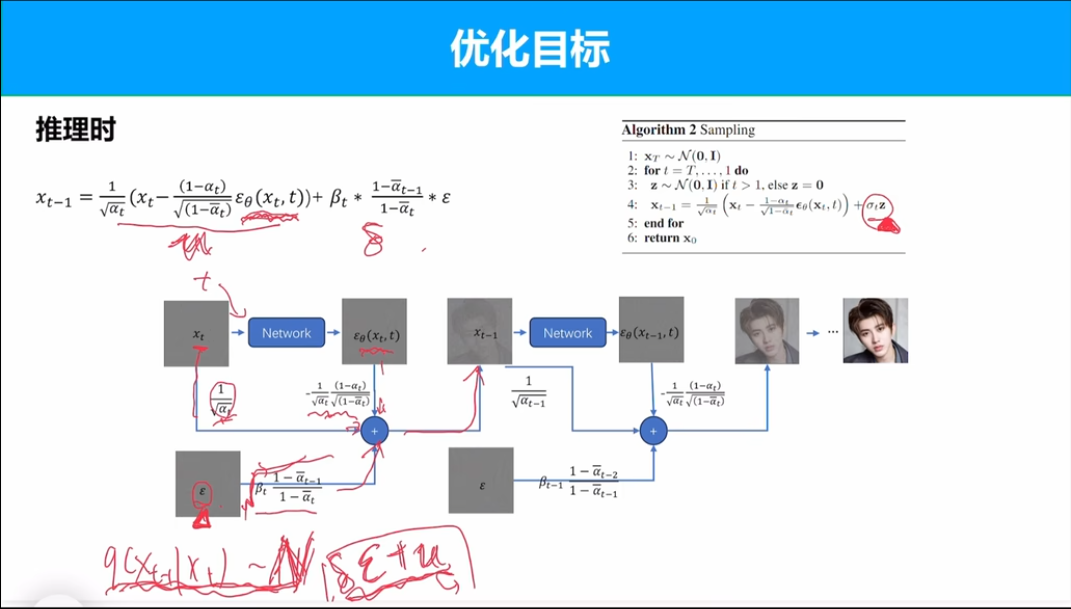
推理过程中增加高斯随机变量z, 保证整体符合高斯分布。
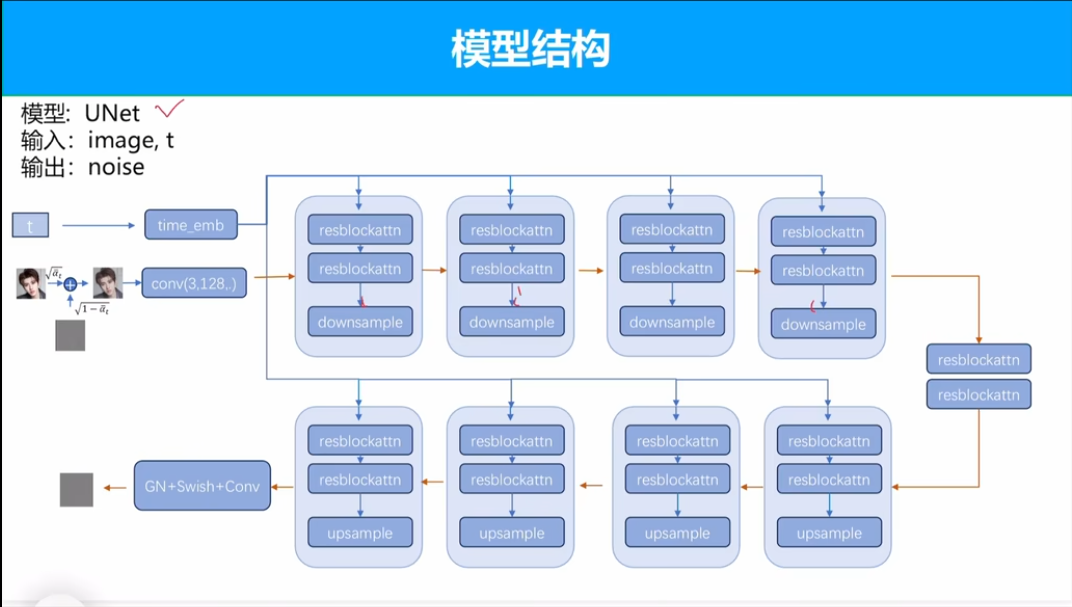

时间嵌入采用标准的位置编码。
总结

文章评论