01背包问题详解
01背包是一种动态规划问题。动态规划的核心就是状态转移方程，本文主要解释01背包状态转移方程的原理。
问题描述
01背包问题可描述为如下问题：
有一个容量为V的背包，还有n个物体。现在忽略物体实际几何形状，我们认为只要背包的剩余容量大于等于物体体积，那就可以装进背包里。每个物体都有两个属性，即体积w和价值v。
问：如何向背包装物体才能使背包中物体的总价值最大？
原始的 01背包
01背包的状态转移方程为
$$
C_{[i][j]} = max(C_{[i – 1][j]}, C_{[i – 1][j – w[i]]} + v_{[j]})
$$
- i代表对i件物体做决策，有两种方式—放入背包和不放入背包。
- j表示当前背包剩余的容量。
转移方程的解释：
创建一个状态矩阵f，横坐标 i 是物体编号，纵坐标 j 为背包容量。
首先将 f 第0行和第0列初始化为0，表示不放物体时最大价值为0 。（物体编号从1开始）
接下来依次遍历f的每一行。如下所示。
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= 0; j--)
{
if (j >= w[i])//如果背包装得下当前的物体
{
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
}
else//如果背包装不下当前物体
{
f[i][j] = f[i - 1][j];
}
}
}
如果背包装得下当前的物体，在遍历过程中分别计算第i件物体放入和不放入背包的价值，取其中大的做为当前的最大价值。
如果背包装不下当前物体那么第i个物体只有不放入背包一种选择。
- 不放入背包时，第i次决策后的最大价值和第i-1次决策时候的价值相同。
-
放入背包时:第i次决策后的价值为 第i-1次决策时候的价值 加上 当前物体的价值v[j]。
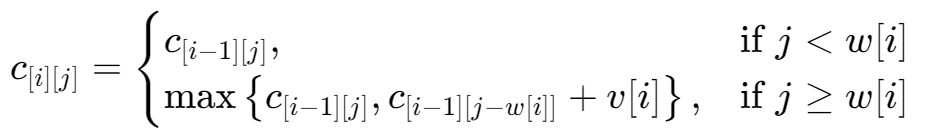
表格举例：
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 0（w，v） | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1（2，3） | 0 | 0 | 3 | 3 | 3 | 3 | 3 |
| 2（3，5） | 0 | 0 | 3 | 5 | 5 | 8 | 8 |
| 3（4，6） | 0 | 0 | 3 | 5 | 6 | 6 | 9 |
#include
#include
using namespace std;
#define max(N1,N2) N1>N2?N1:N2
int main()
{
/*
第一行输入背包容量V和物体的个数n
接下来有n行，每行包含两个数字，分别为该物体的花费和价值
*/
vector w, v;//w为花费，v为价值
vector> f;//f状态矩阵
int V, n;//V背包容量，n物体数
while (cin >> V >> n)
{
w.clear();
v.clear();
f.clear();
w.push_back(0);
v.push_back(0);
//输入原始数据
for (int i = 1; i <= n; i++)
{
int cur_w, cur_v;
cin >> cur_w >> cur_v;
w.push_back(cur_w);
v.push_back(cur_v);
}
//初始化状态矩阵
for (int i = 0; i <= n; i++)
{
vector buff(V + 1, 0);
f.push_back(buff);
}
//动态规划过程
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= 0; j--)
{
if (j >= w[i])
{
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
}
else
{
f[i][j] = f[i - 1][j];
}
}
}
//输出答案
int ans = f[n][V];
cout << ans << endl;
}
return 0;
}
优化空间复杂度的 01背包
未优化时候状态转移方程为
$$
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[j])
$$
遍历过程为
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= 0; j--)
{
if (j >= w[i])
{
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
}
else
{
f[i][j] = f[i - 1][j];
}
}
}
可以发现如下问题：
（1）状态表f的遍历顺序为从第1行开始一行一行遍历，且在遍历第i行时候不会用到第i-2行数据，也就是i-2行及以前的数据没有用了，可以清除。同时，第i-1行的数据每个只会用到一次。
（2）遍历每一行时候只用到当前容量j和j-w[i]的数据，也就是第 i 次遍历只需要 第 i-1 次遍历中容量小于等于 j 的数据 。
所以我们可以按照如下方法优化f的空间复杂度：
$$
f[j] = max(f[j], f[j - w[i]] + v[j])
$$
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= 0; j--)
{
if (j >= w[i])
{
f[j] = max(f[j], f[j - w[i]] + v[i]);
}
else
{
f[j] = f[j];
}
}
}
从本质上说，这种优化方法针对了上述的两个问题：
（1）把遍历第i个物体和遍历第i-1个物体时的最大价值存在一个单元里。更新前f[j]存i-1的价值，更新后f[j]存i的价值。因为用不到i-2及以前的数据所以不需要存。因为以后不会再用到i-1的价值所以被覆盖了没问
（2）j从背包容量V开始遍历，即从大到小遍历，保证了当前f[j]和f[j - w[i]]里面存的是i-1的数据，即等价于f([i])[j] = max(f([i - 1])[j], f([i - 1])[j - w[i]] + v[i])，从而和优化空间复杂度前状态转移方程的原理一致。
但仍存在一些问题，比如
else
{
f[j] = f[j];
}
自己给自己赋值，是无用操作，所以j < w[i]时候什么都不做即可。换句话说，只需要遍历到j >= w[i]，从而得到
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= w[i]; j--)
{
f[j] = max(f[j], f[j - w[i]] + v[i]);
}
}
最终代码如下
/*
#include
#include
using namespace std;
#define max(N1,N2) N1>N2?N1:N2
int main()
{
/*
第一行输入背包容量V和物体的个数n
接下来有n行，每行包含两个数字，分别为该物体的花费和价值
*/
vector w, v;//w为花费，v为价值
vector f;//f状态矩阵
int V, n;//V背包容量，n物体数
while (cin >> V >> n)
{
w.clear();
v.clear();
f.clear();
w.push_back(0);
v.push_back(0);
//输入原始数据
for (int i = 1; i <= n; i++)
{
int cur_w, cur_v;
cin >> cur_w >> cur_v;
w.push_back(cur_w);
v.push_back(cur_v);
}
//初始化状态矩阵
f = vector(V + 1, 0);
//动态规划过程
for (int i = 1; i <= n; i++)
{
for (int j = V; j >= w[i]; j--)
{
f[j] = max(f[j], f[j - w[i]] + v[i]);
}
}
//输出答案
int ans = f[V];
cout << ans << endl;
}
return 0;
}