数据结构C++——最小生成树之Prim算法和Kruskal算法

一、最小生成树的基本概念

最小生成树 ： 在一个连通网的所有生成树中，各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树, 简称为最小生成树。

普里姆 (Prim) 算法 和克鲁斯卡尔 (Kruskal) 算法是两个利用 MST 性质构造最小生成树的算法

MST性质的定义

假设N=(V,{E})是一个连通网，U是顶点集V的一个非空子集。

若(u,v)是一条既有最小权值(代价)的边，其中u∈U，v∈V，则必存在一颗包含边(u,v)的最小生成树。

链接：带你理解MST性质 – 科班小白 – 博客园 (cnblogs.com)

二、最小生成树之Prim算法

（一）Prim算法的实现原理

假设图中的所有顶点和边结点存于U全集集合中，而新建一个集合T用于存放最小生成树的结点。从U集合中的某个顶点开始，不断查找到U-V集合的最小权值边和边所依附的另一个顶点，将此最小权值边和另一个顶点归并入T集合中，在实行完归并操作后，检查此时U-V中的所有结点到刚归入的结点的边的权值是否有小于当前辅助数组单元值lowcost值的情况，若有此情况，则更新辅助数组单元值，使辅助数组的lowcost中永远存放剩余顶点到T集合的最小边权值。

注：此处笔者所写的U-V指的是全集除去归并后的元素后的集合`

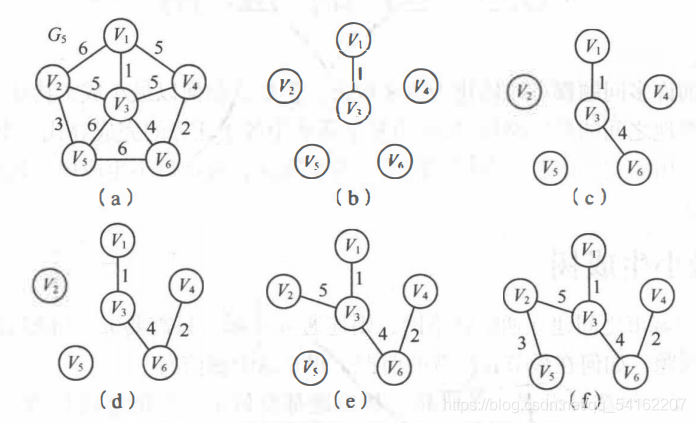
以下是生成最小生成树的图解算法：

（二）Prim算法中的Min函数的实现

算法思路：

1. 函数传参传入辅助数组和图的顶点数
2. 通过for循环寻找$closedge[i].lowcost$值最小的结点编号
3. 最后循环结束，函数返回此编号值

/*--------在辅助数组中找到lowcost最小的顶点-------*/
int Min(MinEdge closedge[],int size) {
    //取最小权值边的顶点位置
    int k = -1;//最后接收最小权值邻接点的下标
    for (int i = 0; i < size; i++) {
        if (closedge[i].lowcost > 0) {//i号顶点并未被归入到生成树中
            int min = closedge[i].lowcost;//设置min中间变量存放最小权值
            for (int j = i; j < size; j++) {
                if (closedge[j].lowcost > 0 && min >= closedge[j].lowcost) {
                    min = closedge[j].lowcost;
                    k = j;
                }
            }
            break;
        }
    }
    return k;
}

（三）Prim算法的代码实现

辅助数组的定义

关于Prim算法的代码实现，笔者有参考这篇文章，笔者就是从中找到的思路，写的真的很不错，链接如下，向大佬致敬：数据结构图最小生成树Prim算法(C语言).

/*-------辅助数组的定义，用来记录从顶点集U到V-U的权值最小的边-------*/
typedef struct 
{
   VerTexType adjvex;//最小边在U中的那个顶点
   ArcType lowcost;//最小边上的权值
}MinEdge;
MinEdge closedge[MVNum];

Prim算法思路：

1. 传入一个顶点编号，生成最小生成树的过程就从这个结点开始。
2. 初始化辅助数字，将辅助数组的adjvex域初始化为传入的结点，lowcost域初始化为该结点到其他顶点的权值，该结点对应的辅助数组lowcost域值初始化为0，表示此顶点已经归入最小生成树集合中。
3. 求出下一个要归并的结点，输出此结点信息和边权值，通过辅助数组的赋值操作，使该结点归并到最小生成树集合中。
4. 新顶点归并到最小生成树集合中后，检查剩余各节点到新归入的结点的边权值是否有小于当前closedge数组的lowcost值的情况，若有此情况，则重新将辅助数组单元值赋值。

/*------------构造最小生成树的Prim算法----------*/
void MiniSpanTree_Prim(AMGraph G, VerTexType u) {
    //无向网G以邻接矩阵形式存储，从顶点u出发构造G的最小生成树T，输出T的各条边
    int k = LocateVex(G, u);//k为顶点u的下标
    for (int j = 0; j < G.vexnum; j++) {
        //对V-U的每一个顶点vj，初始化closedge[j]
        closedge[j].adjvex = u;//{adjvex,lowcost}
        closedge[j].lowcost = G.arcs[k][j];
    }
    closedge[k].lowcost = 0;//初始,U={u}
    for (int i = 1; i < G.vexnum; i++) {
        //选择其余n-1个结点，生成n-1条边（n=G.vexnum）
        int k = Min(closedge,G.vexnum);
        //求出T的下一个结点；第k个顶点,closedge[k]中存有当前最小边
        ArcType u0 = closedge[k].lowcost;//u0为最小边的一个顶点,u0属于u
        VerTexType v0 = G.vex[k];//v0为最小边的另一个顶点，v0属于V-U
        cout << u0 << " " << v0 << endl;//输出当前的最小边(u0,v0);
        closedge[k].lowcost = 0;//第k个顶点并入U集
        for (int j = 0; j < G.vexnum; j++) {
            if (G.arcs[k][j] < closedge[j].lowcost)//新顶点并入U后重新选择最小边
            {
                closedge[j].adjvex = G.vex[k];
                closedge[j].lowcost = G.arcs[k][j];
            }
        }
    }
}        

（四）测试的完整代码

测试代码采用了邻接矩阵表示法，由于笔者在之前的文章中已介绍过邻接矩阵和邻接表的创建，因此，关于这部分知识，笔者不再赘述。想了解相关内容，读者可移步到此文章，共同学习！：数据结构C++------图的邻接矩阵和邻接表

#include
#include
using namespace std;
#define MVNum 100
#define MAXInt 32767//定义无穷大
typedef  string VerTexType;
typedef int ArcType;
/*----------图的邻接矩阵表示法存储结构---------*/
typedef struct {
    int arcnum, vexnum;//顶点数和边数
    VerTexType vex[MVNum];//定义存储顶点的数组
    ArcType arcs[MVNum][MVNum];//定义存储边的数组
}AMGraph;
/*-------辅助数组的定义，用来记录从顶点集U到V-U的权值最小的边-------*/
typedef struct 
{
    VerTexType adjvex;//最小边在U中的那个顶点
    ArcType lowcost;//最小边上的权值
}MinEdge;
MinEdge closedge[MVNum];
/*----------在顶点表中找到传入顶点的位置---------*/
int LocateVex(AMGraph G, VerTexType v) {
    //遍历顶点表，返回某顶点在顶点表中的位置下标
    for (int i = 0; i < G.vexnum; i++) {
        if (G.vex[i] == v)//在顶点表中找到了顶点v
            return i;//返回其下标
    }
    return -1;//没找到返回-1
}
/*---------采用邻接矩阵表示法创建无向网-------*/
void CreateUDN(AMGraph& G) {
    //采用邻接矩阵表示法，创建无向网
    int i = 0, j = 0, k = 0, w;
    cin >> G.vexnum >> G.arcnum;//输入总顶点数，总边数
    for (i = 0; i < G.vexnum; i++)//依次输入点的信息
        cin >> G.vex[i];
    for (i = 0; i < G.vexnum; i++)//初始化邻接矩阵
        for (j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = MAXInt;
    for (k = 0; k < G.arcnum; k++) {
        VerTexType v1, v2;//定义两个顶点v1,v2
        cin >> v1 >> v2 >> w;
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);//确定v1和v2在G中的位置，即顶点数组的下标
        G.arcs[i][j] = G.arcs[j][i] = w;
    }
}
/*--------在辅助数组中找到lowcost最小的顶点-------*/
int Min(MinEdge closedge[],int size) {
    //取最小权值边的顶点位置
    int k = -1;//最后接收最小权值邻接点的下标
    for (int i = 0; i < size; i++) {
        if (closedge[i].lowcost > 0) {//i号顶点并未被归入到生成树中
            int min = closedge[i].lowcost;//设置min中间变量存放最小权值
            for (int j = i; j < size; j++) {
                if (closedge[j].lowcost > 0 && min >= closedge[j].lowcost) {
                    min = closedge[j].lowcost;
                    k = j;
                }
            }
            break;
        }
    }
    return k;
}
/*------------构造最小生成树的Prim算法----------*/
void MiniSpanTree_Prim(AMGraph G, VerTexType u) {
    //无向网G以邻接矩阵形式存储，从顶点u出发构造G的最小生成树T，输出T的各条边
    int k = LocateVex(G, u);//k为顶点u的下标
    for (int j = 0; j < G.vexnum; j++) {
        //对V-U的每一个顶点vj，初始化closedge[j]
        closedge[j].adjvex = u;//{adjvex,lowcost}
        closedge[j].lowcost = G.arcs[k][j];
    }
    closedge[k].lowcost = 0;//初始,U={u}
    for (int i = 1; i < G.vexnum; i++) {
        //选择其余n-1个结点，生成n-1条边（n=G.vexnum）
        int k = Min(closedge,G.vexnum);
        //求出T的下一个结点；第k个顶点,closedge[k]中存有当前最小边
        ArcType u0 = closedge[k].lowcost;//u0为最小边的一个顶点,u0属于u
        VerTexType v0 = G.vex[k];//v0为最小边的另一个顶点，v0属于V-U
        cout << u0 << " " << v0 << endl;//输出当前的最小边(u0,v0);
        closedge[k].lowcost = 0;//第k个顶点并入U集
        for (int j = 0; j < G.vexnum; j++) {
            if (G.arcs[k][j] < closedge[j].lowcost)//新顶点并入U后重新选择最小边
            {
                closedge[j].adjvex = G.vex[k];
                closedge[j].lowcost = G.arcs[k][j];
            }
        }
    }
}
int main() {
    AMGraph G;
    CreateUDN(G);
    int v = 0;
    MiniSpanTree_Prim(G,G.vex[v]);
    return 0;
}

测试结果

输入：
6 10
v1 v2 v3 v4 v5 v6
v1 v2 6
v1 v3 1
v1 v4 5
v2 v3 5
v3 v4 5
v2 v5 3
v3 v5 6
v3 v6 4
v4 v6 2
v5 v6 6

输入数据构建的图

此输出结果为从0号结点v1开始，生成最小生成树，则归入的生成树结点及两结点依附的边权值：

输出：
1 v3
4 v6
2 v4
5 v2
3 v5

三、最小生成树之Kruskal算法

（一）Kruskal算法的实现原理

设置两个辅助数组Edge和Vexset，Edge用来存储边权值及边依附的始点和终点，Vexset用来存储各顶点的连通分量值（Vexset的单元值相同则表明顶点属于同一个连通分量）。根据输入的边数和点数创建无向图的邻接矩阵，此处不同的是，需要将输入的边信息存储到辅助数组Edge中去。将Edge数组中的元素按边权值从小到大排序，初始化Vexset数组。按照边权值从小到大的顺序，依次使边依附的终点和始点属于同一个连通分量，直到遍历结束边信息，此时最小生成树的所有结点同属于一个连通分量，最小生成树构造完毕。

图解算法

Kruskal算法的实现过程:

（二）Krusal算法的代码实现

辅助数组的定义

/*-----------辅助数组Edges的定义--------------*/
typedef struct edge{
   VerTexType Head;//边的始点
   VerTexType Tail;//边的终点
   ArcType lowcost;//边上的权值
}Edgea;
Edgea Edge[MVNum];
/*---------辅助数组Vexset的定义------------*/
int Vexset[MVNum];

Kruskal算法思路：

1. 将辅助数组Edge中的元素按权值从小到大排序
2. 初始化辅助数组Vexset，使其中结点本身的结点编号，表明各顶点自称一个连通分量
3. 从0号单元开始，依次获取按边权值排好序的边Edge[i]依附的始点Head和终点Head在顶点表中的位置下标
4. 获取边Edge[i]的始点和终点所在的连通分量
5. 若始点和终点不属于同一个连通分量，则输出始点和终点及其所依附的边，后将始点和终点的Vexset数组值更新，表明两点属于同一连通分量

/*----------Kruskal算法的代码实现----------*/
void MiniSpanTree_Kruskal(AMGraph& G) {
    //无向网G以邻接矩阵形式存储，构造G的最小生成树T，输出T的各条边
    sort(Edge, Edge + G.arcnum, cmd);//将数组Edge中的元素按权值从小到大排序
    for (int i = 0; i < G.vexnum; i++)//辅助数组，表示各顶点自成一个连通分量
        Vexset[i] = i;
    for (int i = 0; i < G.arcnum; i++) {//依次查看数组Edge中的边
        int v1, v2 = 0;
        v1 = LocateVex(G, Edge[i].Head);//v1为边的始点Head的下标
        v2 = LocateVex(G, Edge[i].Tail);//v2为边的终点Tail的下标
        int vs1, vs2 = 0;
        vs1 = Vexset[v1];//获取边Edge[i]的始点所在的连通分量vs1
        vs2 = Vexset[v2];//获取边Edge[i]的终点所在的连通分量vs2
        if (vs1 != vs2) {//边的两个顶点分属不同的连通分量
            cout << Edge[i].Head <<" "<< Edge[i].Tail <<" "<< Edge[i].lowcost << endl;//输出此边
            for (int j = 0; j < G.vexnum; j++) {//合并vs1和vs2两个分量，即两个集合统一编号
                if (Vexset[j] == vs2) Vexset[j] = vs1;//集合编号为vs2的都改成vs1
            }
        }
    }
}

（三）测试的完整代码

测试代码采用了邻接矩阵表示法，由于笔者在之前的文章中已介绍过邻接矩阵和邻接表的创建，因此，关于这部分知识，笔者不再赘述。想了解相关内容，读者可移步到此文章，共同学习！：数据结构C++------图的邻接矩阵和邻接表

#include
#include
#include
using namespace std;
#define MVNum 100
#define MAXInt 32767//定义无穷大
typedef  string VerTexType;
typedef int ArcType;
/*----------图的邻接矩阵表示法存储结构---------*/
typedef struct {
    int arcnum, vexnum;//顶点数和边数
    VerTexType vex[MVNum];//定义存储顶点的数组
    ArcType arcs[MVNum][MVNum];//定义存储边的数组
}AMGraph;
/*-----------辅助数组Edges的定义--------------*/
typedef struct edge{
    VerTexType Head;//边的始点
    VerTexType Tail;//边的终点
    ArcType lowcost;//边上的权值
}Edgea;
Edgea Edge[MVNum];
/*---------辅助数组Vexset的定义------------*/
int Vexset[MVNum];
/*----------在顶点表中找到传入顶点的位置---------*/
int LocateVex(AMGraph G, VerTexType v) {
    //遍历顶点表，返回某顶点在顶点表中的位置下标
    for (int i = 0; i < G.vexnum; i++) {
        if (G.vex[i] == v)//在顶点表中找到了顶点v
            return i;//返回其下标
    }
    return -1;//没找到返回-1
}
/*---------采用邻接矩阵表示法创建无向网-------*/
void CreateUDN(AMGraph& G) {
    //采用邻接矩阵表示法，创建无向网
    int i = 0, j = 0, k = 0, w;
    cin >> G.vexnum >> G.arcnum;//输入总顶点数，总边数
    for (i = 0; i < G.vexnum; i++)//依次输入点的信息
        cin >> G.vex[i];
    for (i = 0; i < G.vexnum; i++)//初始化邻接矩阵
        for (j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = MAXInt;
    for (k = 0; k < G.arcnum; k++) {
        VerTexType v1, v2;//定义两个顶点v1,v2
        cin >> v1 >> v2 >> w;
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);//确定v1和v2在G中的位置，即顶点数组的下标
        G.arcs[i][j] = G.arcs[j][i] = w;
        Edge[k].Head = v1;
        Edge[k].Tail = v2;
        Edge[k].lowcost = w;
    }
}
/*-----获取图的边数---------*/
int getArcnum(int n) {//获取图的边数
    return n;
}

bool cmd(edge a,edge b) {
    return a.lowcost < b.lowcost;
}
/*----------Kruskal算法的代码实现----------*/
void MiniSpanTree_Kruskal(AMGraph& G) {
    //无向网G以邻接矩阵形式存储，构造G的最小生成树T，输出T的各条边
    sort(Edge, Edge + G.arcnum, cmd);//将数组Edge中的元素按权值从小到大排序
    int sum = 0;
    for (int i = 0; i < G.vexnum; i++)//辅助数组，表示各顶点自成一个连通分量
        Vexset[i] = i;
    for (int i = 0; i < G.arcnum; i++) {//依次查看数组Edge中的边
        int v1, v2 = 0;
        v1 = LocateVex(G, Edge[i].Head);//v1为边的始点Head的下标
        v2 = LocateVex(G, Edge[i].Tail);//v2为边的终点Tail的下标
        int vs1, vs2 = 0;
        vs1 = Vexset[v1];//获取边Edge[i]的始点所在的连通分量vs1
        vs2 = Vexset[v2];//获取边Edge[i]的终点所在的连通分量vs2
        if (vs1 != vs2) {//边的两个顶点分属不同的连通分量
            cout << Edge[i].Head <<" "<< Edge[i].Tail <<" "<< Edge[i].lowcost << endl;//输出此边
            for (int j = 0; j < G.vexnum; j++) {//合并vs1和vs2两个分量，即两个集合统一编号
                if (Vexset[j] == vs2) Vexset[j] = vs1;//集合编号为vs2的都改成vs1
            }
        }
    }
}
int main() {
    AMGraph G;
    CreateUDN(G);
    MiniSpanTree_Kruskal(G);
    return 0;
}

输入：
6 10
v1 v2 v3 v4 v5 v6
v1 v2 6
v1 v3 1
v1 v4 5
v2 v3 5
v3 v4 5
v2 v5 3
v3 v5 6
v3 v6 4
v4 v6 2
v5 v6 6

输入数据构建的图

此输出结果为：加边的先后顺序，输出格式表头为（始点 终点 边权值）

输出：
v1 v3 1
v4 v6 2
v2 v5 3
v3 v6 4
v2 v3 5

---

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

原文链接：https://blog.csdn.net/qq_54162207/article/details/117535738