影像生成模型共同目标
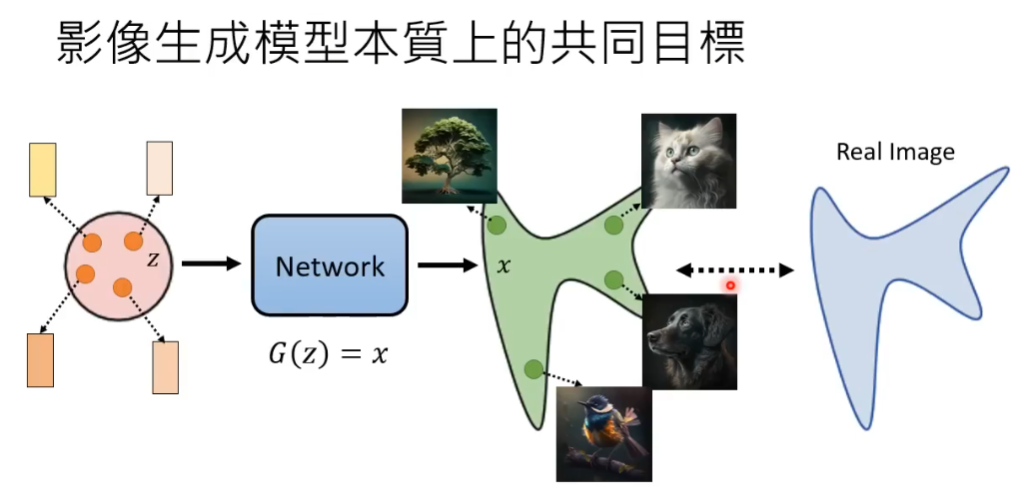
在一个简单样本分布中任意向量样本,通过神经网络生成复杂样本分布。这种生成的分布和真实情况作比较。
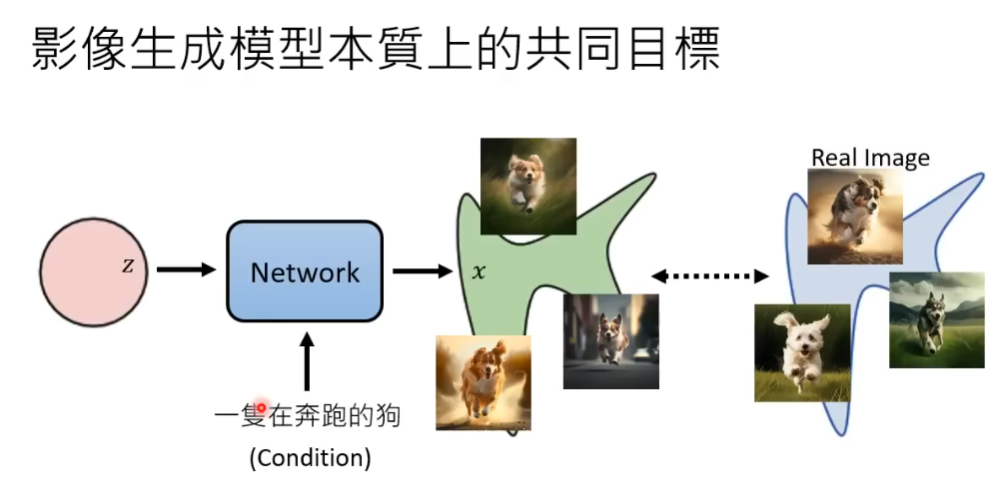
对于文字生成图片的模型来说,输入不仅有简单样本分布的样本向量,文字也可以作为输入向量。
最大似然估计
最大似然估计(Maximum Likelihood Estimation,MLE)是一种统计学中常用的参数估计方法。这种方法的基本思想是:给定一个概率模型和一些观测数据,我们需要找到模型参数的最佳值,使得在这些参数下,观测数据出现的概率(也称为似然)最大。
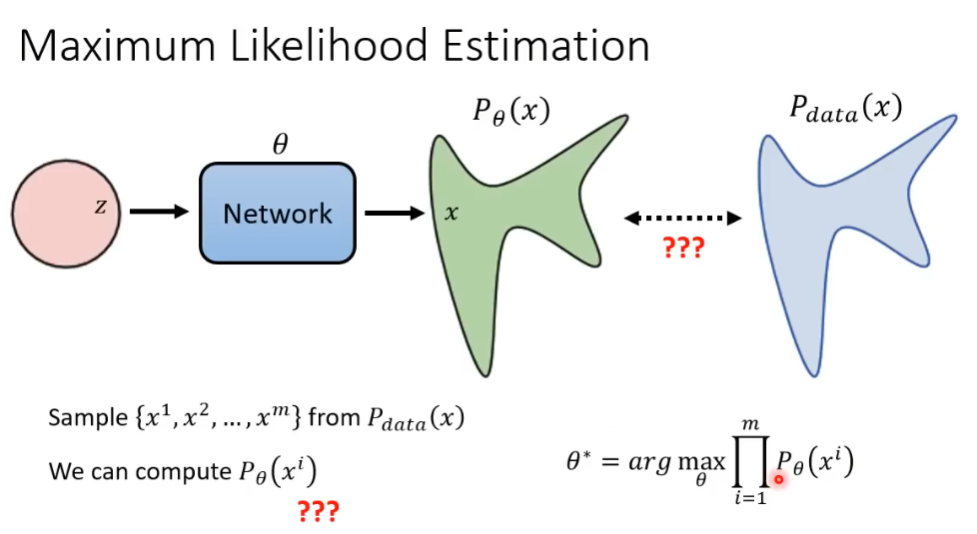
假设从现实世界中采样出 x^1\rightarrow x^m 共 m 条样本向量,通过带参数 \theta 的神经网络,对于每一个样本 x,输出得到预测情况下该样本实现的概率 P_{\theta}(x).对于所有 m 条向量,根据最大似然估计得出最佳参数 {\theta^*}.
KL 散度
KL 散度(Kullback-Leibler divergence),可以以称作相对熵(relative entropy)或信息散度(information divergence)。KL 散度的理论意义在于度量两个概率分布之间的差异程度,当 KL 散度越大的时候,说明两者的差异程度越大;而当 KL 散度小的时候,则说明两者的差异程度小。如果两者相同的话,则该 KL 散度应该为 0。

变分自编码器
变分自编码器(Variational Auto-Encoders,VAE)是一种结合了概率图模型与深度神经网络的生成模型。与传统的自编码器不同,VAE 不仅关注于数据的重建,还致力于学习数据的潜在分布,从而能够生成逼真的新样本。
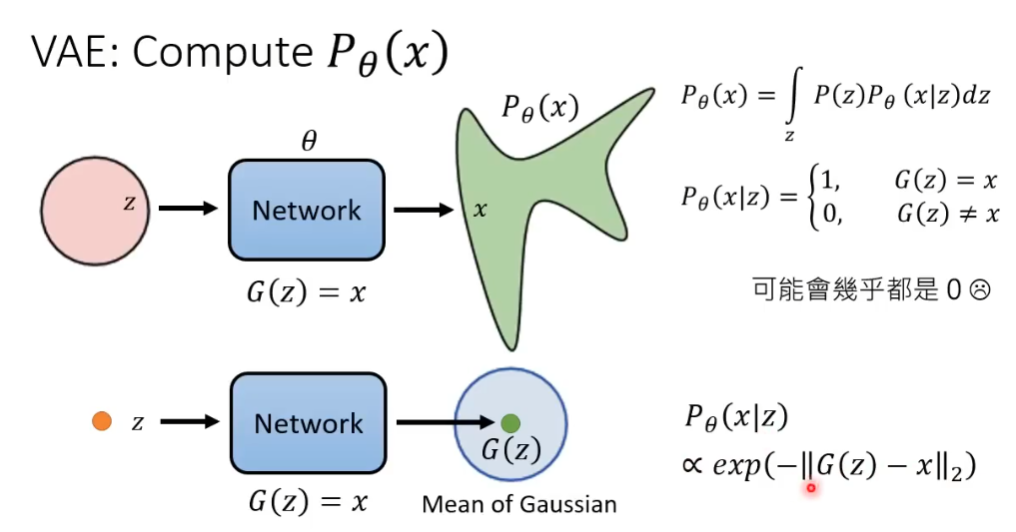
在 VAE 中如果计算 P_{\theta}(x|z),最初假设二元分类,相同为 1 不同为 0,但是结果可能都是零。
所以VAE 通过引入高斯分布对 P_{\theta}(x|z) 建模,将生成样本 G(z) 视为均值,从而构建了与输入 x 的连续相似性度量,真实样本 x 与 G(z) 的距离正比于 P_{\theta}(x|z)。

为了便于计算,VAE 拆分成 \int_{z}q(z|x)log\left(\frac{P(z,x)}{q(z|x)}\right)dz 和 KL\left(q(z|x)||P(z|x)\right),KL 散度为非负值,最后转为计算 logP_{\theta}(x) 的下界。下届值越大,P_{\theta}(x) 的值就越大,证明预测结果越好。
扩散模型
DDPM(Denoising Diffusion Probabilistic Models)
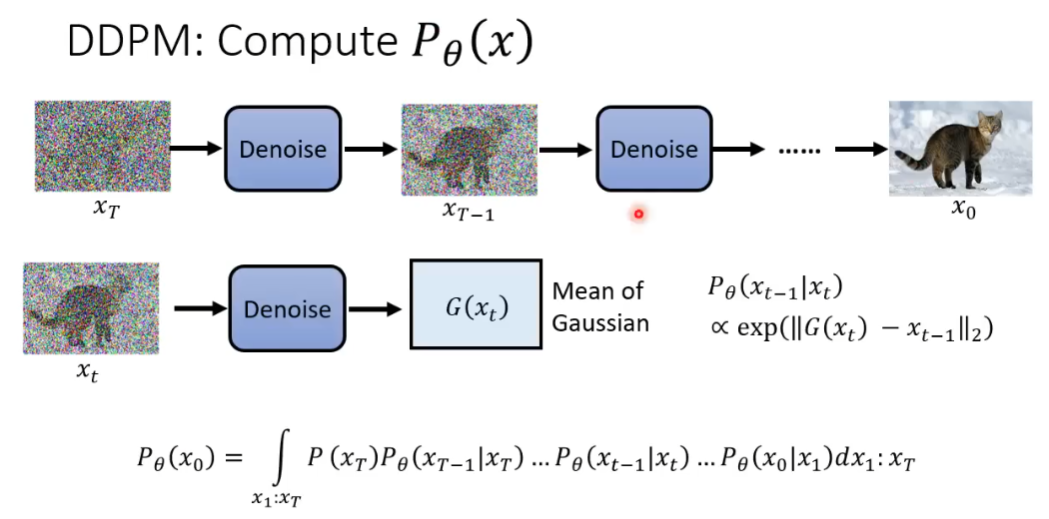
对于扩散模型,类似VAE,输入x_t经过Denoise神经网络,输出为x_t的高斯分布的均值,正比于真实情况和预测值的距离。最终生成x_0真实图像的概率由扩散过程中的每一步(x_1:x_T)预测概率连乘积分得到。

同样在计算过程中,我们简化为计算logP_{\theta}(x_0)的下届的最大值。对于输入样本x_0,输出为x_1到x_T,对照扩散模型中的前向过程。
文章评论